المفاهيم الأوّلية للنظرية اللسانية

في مقالنا الأول بعنوان "اللغة والعلم والإنسان" قلنا إنّ الدكتور الفاسي الفهري يُعرّف النظرية اللسانية في كتابه "اللسانيات واللغة العربية" بقوله: " النظرية اللسانية، كسائر النظريات، هي بناء عقلي يتوق إلى ربط أكبر عدد من الظواهر الملاحظة بقوانين خاصة تُكوِّن مجموعة متسقة يحكمها مبدأ عام هو مبدأ التفسير. ويمكن تمثّلها كمجموعة من المفاهيم الأساسية ومجموعة من المُسلَّمات تُسْتَنتَج منها النتائج التفسيرية للنظرية. وكل المفاهيم اللسانية للنظرية تُعرَّف انطلاقـاً من المفاهيم الأساسية التي تُعتبر أوّلية. وهناك عدة إمكانيات لاختيار مجموعة الأوّليات التي يُبنى عليها النسق الاستنتاجي أو الإكسيوميّة (البدهية) التي تُشتق منها القضايا المبرهَنة ".
ونحن هنا سنعرض للمفاهيم المنطقية الأوّلية المعروفة للجميع بالبداهة لعدم وجود عاقل لا يتعامل معها بالفطرة.
من أوّل هذه المفاهيم مفهوم " العنصر Element ".
وهو يمثل أي شيء يمكن تحسسه أو تصوره مهما كان، والفكر والحياة يفيضان بالعناصر، فالإنسان عنصر، وزيد عنصر، والكرة الأرضية عنصر، والذرّة عنصر، والمنزل عنصر، والأفكار والمشاعر عناصر أيضاً مع أنها نسبية.
وحيث أن كل عنصر عبارة عن العناصر التي يتشكل منها، ويُشكِّل بدوره مع عناصر أخرى عنصراً جديداً، فإن العناصر تتشكل مع أو من بعضها بعضاً بواسطة عملية وحيدة هي:
التشكيل أو " العملية Operation  " وهي المفهوم الثاني، الذي سنُطلق عليه مبدأ وحدة الخَلْق.
إن مبدأ وحدة الخَلْق أو التشكيل بين عنصرين يُعْرَف بعملية الترابط المنطقية Conjunction، أو عملية الضرب المنطقية. ونرمز لها بالرمز " و " ونقرأ: مرتبط مع أو يتشكل مع والكثير يقرأ " و ". والواو هنا رمز لعملية منطقية بحتة هي عملية تشكيل لعنصر جديد من عنصرين.
فمثلاً " الرجال و النساء " يُشكِّلون الجنس البشري، ولا يمكن لهذا الجنس أن يتشكل من أحدهما ولابد من وجودهما معاً، وكذلك " بنية الإلكترونات و بنية النواة " تُشكّلان بنية الذرّة، وهكذا.
والعملية بين عدة عناصر تُعطي دوماً عنصراً جديداً متشكلاً من هذه العناصر، لذا نُسميها في كثير من الأحيان: قانون التشكيل.
أمّا المفهوم الثالث فهو مفهوم " العلاقة Relation  ".
الذي نُطلق عليه: مبدأ الهويَّة أو مبدأ وحدة الوجود، وهو يعني أن وجود العنصر وحيد، فالعنصر لا يمكن أن يكون إلاّ ذاته أي بالرمز a = a. فالعلاقة تقوم بتمييز العناصر عن بعضها بعضاً وإعطائها هويَّتها، بعد أن تقوم العملية بتشكيلها أو خَلْقها. والعلاقة لا تعطي عناصر جديدة.
فمثلاً علاقة " أكبر من" تقوم بترتيب عنصرين بالنسبة لبعضهما بعضاً وبالتالي تمييزهما، ولا تعطي عنصراً جديداً.
في أي من مجالات الفكر والحياة نقابل عناصر جديدة يتوجب علينا تعريفها، لنتمكن من التفاعل معها.
وعندما نُعرِّف عنصراً ما، يجب تعريفه بعناصر مُعرَّفة أو عناصر أساسية معروفة للجميع بالفطرة.
فمثلاً عند تعريف موقع ما لإنسان ما للاستدلال عليه؛ فإننا نبني تعريفنا على موقع معروف له، ثم نتابع الدلالة بذكر أشياء أو مواقع معروفة أيضاً.
نلاحظ أنه يتم التعرُّف إلى العنصر بمعرفة أجزائه التي يتشكل منها، ومعرفة علاقات هذه الأجزاء فيما بينها، وكذلك معرفة علاقاته مع العناصر الأخرى أي تمييزه بينها.
فتعريف عنصر: هو العملية أو العمليات التي يتشكل منها (من أجزائه) وهو أيضاً علاقة أو علاقات هذا العنصر مع العناصر الأخرى (ومنها أجزاؤه).
ولأول مرّة نقول: إن مفهومي " العملية و العلاقة " هما تعميم لمفهومي " الكتلة و الطاقة " الفيزيائيين.
فالكتلة هي تشكيل للعنصر الفيزيائي من أجزائه (المتشكِّلة)، والطاقة بين هذه الأجزاء أو الطاقة بين هذا العنصر والعناصر الأخرى، تمثل علاقات الأجزاء ببعضها أو علاقات العنصر مع العناصر الأخرى.
فالعنصر عبارة عن العناصر والعمليات والعلاقات التي تقوم بتعريفه. ونُسمي ذلك " الصيغة Formula "، وهي الطريقة التي يُعبِّر فيها العنصر عن ذاته. والصيغة بأكملها طبعاً يُنظر إليها على أنها العنصر الذي تُعبِّر عنه. ومنه نؤكّد أن الصيغة والعنصر اسمان لمسمى واحد.
 بدهي أيضاً أن كل عنصر يقبل الوصف بالوجود (الحضور) أم الغياب، اللذَين نرمز لهما بالرمزين (1 ، 0) على الترتيب، فيدل الأول على حضور العنصر ويدل الثاني على غيابه. ونُسمي الرمزين (1 ، 0) بقيم التمييز.
إن ما سبق يقودنا إلى مفهومي المكان والزمان اللذين نعرضهما كذلك لأول مرّة كما يلي:
نُسَلِّم بأن العنصر يخضع لصيغة المكان، وتعني أن العنصر يجب أن يخضع (يوصف) لإحدى الحالتين:
" الحضور " أم " الغياب ". (يجب الانتباه إلى أن غياب عنصر في مكان ما، يعني وجوده في مكان آخر، فالعنصر لا ينعدم ولا يوجد من العدم).      
ونُسمي هذا المفهوم أيضاً بقانون الثالث المرفوع أو المرفوض، لعدم توفر احتمال ثالث لحالة العنصر، لأنه يخضع إما لحالة الوجود وإما لحالة الغياب، ولا ثالث غيرهما.
ونُسَلِّم أيضاً بأن العنصر يخضع لصيغة الزمان، وتعني أن العنصر لا يمكن أن يخضع (يوصف) لحالتي الوجود والغياب معاً بآن واحد، بل ينبغي وجود التلاحق في هذا، فالحضور أولاً ثم الغياب أم الغياب أولاً ثم الحضور.
في الواقع إن التشكيل أو مبدأ وحدة الخلق، يتجلى في مفهوم المكان؛ ويتجلى عن العلاقة (الترتيب) أو مبدأ وحدة الوجود (الهويّة)، مفهوم الزمان. ومن الواضح أنه لولا التشكيل والترتيب (العلاقة) لن يكون المكان والزمان.
ومن الجدير بالملاحظة أنه فيزيائياً، ووفقاً للنظرية النسبية العامة لأينشتاين، لن يتواجد المكان والزمان، في حال انعدام الكتلة والطاقة (مادة الكون).
وباختصار كما قالت العرب: " النقيضان لا يرتفعان ولا يجتمعان ".
وإنهما لا يرتفعان تحقيقاً لصيغة المكان، ولا يجتمعان تحقيقاً لصيغة الزمان.
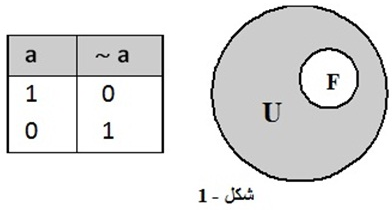
والآن لتكن لدينا صيغة العنصر F من المجموعة U، نُمَثِّل حضور أو وجود العنصر F، برسم حدود هذا العنصر داخل المجموعة U كما في الشكل ( 1 ).
وعندها سيكون غيابه مُمَثلاً بمتممة F بالنسبة إلى U، وهي المساحة المظلَّلة بين حدود العنصرين.
(لأن المساحة المظلَّلة الممثِّلة للمتمّمة لا يوجد فيها F، وبالتالي يكون غائباً فيها، ولا يكون موجوداً إلا في المساحة (المكان) المخصصة له).
من الواضح الآن أننا عندما ننظر إلى ساحة (مكان) F فإننا نتعرَّف شكله (أي تشكيله، أي العناصر التي تقوم بتشكيله)؛ ولكن عندما ننظر إلى ساحة (مكان) متمّمة F (المظلَّلة)، فإننا نتعرَّف شكل العناصر الموجودة فيها، وهي غير F؛ ولكن معرفتنا بشكل عناصر المتمّمة، يقودنا لتمييز أي عنصر ليس من المتممة؛ وبالتالي نستطيع تمييز F.
(ويجب أن نلاحظ أن تمييز F لا يعني معرفتنا بشكله، لأن التمييز يعتمد على معرفتنا بساحة المتممة، بينما معرفتنا لشكله تقتضي معرفتنا بساحته هو).
إن التمييز أو التوصيف (الصفة) لعنصر، هو معرفة شكل المتممة له وبذا نستطيع تمييزه، ويأخذ F القيمة ( 1 )، بينما متممة F تأخذ القيمة ( 0 )، لأننا أمام حضور وغياب بالنسبة إلى F.
ومعرفة شكل العنصر فقط دون معرفة شكل متممته لا يؤدي إلى تمييزه (معرفة صفته)، فالتمييز يحتاج دوماً لجملة مقارنة تتمثَّل بالمتمّمة؛ فمثلاً تنتفي صفة الجمال إذا لم يكن هناك القبح، ولن نستطيع تمييز العنصر الجميل عندها بانتفاء وجود العنصر المتمم الآخر.
منه نرى أن معرفتنا بأي عنصر تندرج في واحدة من الاحتمالات التالية: معرفة الشكل، أم معرفة الصفة (القدرة على التمييز)، أم معرفة الشكل والصفة معاً، أم انعدام معرفة الشكل والصفة معاً.
أي بلغة رياضية: معرفة F، أم معرفة متمّمة F، أم معرفة F ومتمّمته، أم انعدام معرفة F ومتمّمته. ولا توجد حالة خامسة للتعريف بالعنصر.
وبالتالي فإن مفهومي " العملية والعلاقة " اللذين يعنيان " الشكل والصفة "، يؤديان إلى أن أي عنصر يكون من وجهة نظر المعرفة به (بالنسبة لمراقب ما)، في احتمال من الاحتمالات الأربعة التالية:
1 - شكل فقط.
2 - صفة فقط.   
3 - شكل وصفة معاً.
4 – لا شكل ولا صفة له معاً.
نرمز للعناصر عموماً بأحرف مثل: a ، b ، c ، ... الخ.
إن العناصر حسب صيغة المكان لابد أن تأخذ إحدى الحالتين: الوجود أم الغياب.
وباستخدام قيم التمييز نقول لابد أن تأخذ إحدى القيمتين ( 1 ، 0 ).
والآن ليكن لدينا العنصر a، نرمز للعنصر الذي يأخذ قيم تمييز مغايرة لقيم a بالرمز: a ~ ، ونقرأ: نفي a حيث نُسمي الرمز ( ~ ) بالنفي. ومن الواضح أن  a~ صيغة عنصر جديد.
وحسب صيغة المكان: إذا كان العنصر a موجوداً في مكان (ساحة) ما، فهذا يعني أن العنصر  a~ غائب في ذلك المكان. (ويكون موجوداً في مكان (ساحة) آخر، كما هو واضح من الشكل-1).
وحسب صيغة الزمان، فإنه عندما تتغير قيم التمييز: إذا كان العنصر a غائباً في مكان (ساحة) ما، فهذا يعني أن العنصر  a~ موجود في ذلك المكان.
ونستطيع تلخيص ما سبق بجدول يُعْرَف بجدول التمييز أو الحقيقة، وهو الجدول المرفق.  
وقد كتبنا الجدول على سطرين، لأن كل سطر يُمثِّل حالة من حالتي الوجود أم الغياب حسب صيغة المكان؛ ولا نستطيع دمج الحالتين في سطر واحد، لأنهما لا يجتمعان معاً للعنصر الواحد، حسب صيغة الزمان.
فالعنصر a إما أن يأخذ قيمة التمييز ( 1 )، وعندها سيأخذ العنصر  a~ قيمة التمييز ( 0 )، وهذا ما يمثله السطر الأول من الجدول. وإما أن يأخذ a قيمة التمييز ( 0 )، وعندها سيأخذ  a~ قيمة التمييز (1  )، وهذا ما يمثله السطر الثاني من الجدول. وليس هناك احتمال ثالث لحالة العنصر a.
وأخيراً فإننا نُسمي العنصر a~ ثنْويَّة أو مزدوجة العنصر a، والعكس بالعكس.
ونلخص ما سبق بأن: العنصر عبارة عن شكل وصفة، يأخذ شكله وفق مبدأ وحدة الخلق، ويتميّز وفق مبدأ الهويّة. وبهما يحصل على مكانه وزمانه. وعلى أساس ذلك يكون حاضراً أم غائباً، بحيث يتحقق من ذلك مبدأ الثالث المرفوع ومبدأ عدم التناقض.
إن التشكيل والتوصيف، ومفهومي وحدة الخلق والهويّة، وصيغتي المكان والزمان، ومقولتي الحضور والغياب، ومبدأي الثالث المرفوع وعدم التناقض؛ هي ثنائيات متكافئة مثنى مثنى. يمكن أن تحلّ أية ثنائية منها مكان الأخرى.